アルゴリズムとダンスの関係性は、一般的にはコンピューターで生成された振付を連想させがちですが、実際には、アルゴリズムは本質的に動きの「手順」を示すものであり、どのように動くかを具体的に指示します。この点で、アルゴリズムは振付と同義と言えるでしょう。
Contents
ポストモダンダンスとアルゴリズムの適用
この概念を明確にダンスに適用したのは、1960年代のアメリカのポストモダンダンス、特にジャドソン・チャーチ・グループからです。彼ら以前にも、バレエの巨匠ジョージ・バランシンのように、参加するダンサーの人数によって同一の振付を用いながらも、フォーメーションを変化させる表現は実在しましたが、ジャドソン・チャーチ・グループでは「タスク」という概念を用いて、条件に応じて独立して機能する「動きの指示」を中心に振付を構築する作品が出てきます。この革新的なアプローチは、同時期に活動していたアンナ・ハルプリンの影響も受けています。
ジャドソン・ダンス・グループのパフォーマンスは、従来の権威的なステージダンスの概念を覆し、多様な実験を行いました。この取り組みは、ダンスの民主化をもたらし、誰もが参加できる新しい表現形態も生み出しました。イヴォンヌ・レイナーが提唱したタスクベースの振付や、シモーヌ・フォルティらによる人間の群衆行動をシンプルなルールで探求する試みなど、従来のダンスでは考えられなかった多くの要素が解放されました。
コンピューターサイエンスとダンスの交差点
一方、コンピューターサイエンスの分野では、ジョン・コンウェイのライフゲームや、クレイグ・レイノルズのBoidsプログラムなど、生命的な振る舞いや群れの動きをシミュレートするアルゴリズムが開発されてきました。統計学におけるランダムウォークの概念も、動きのアルゴリズム的研究の一例と言えるでしょう。
近年、CPUの速度限界や量子コンピューターの発展といった時代の動向があり、従来のノイマン型アーキテクチャを超えた新たな計算方法の探索が進んでいます。その中でも、フィジカルコンピューティングは、コンピューターの原理を根本から再考する動きとして注目されています。
新たな計算方法の探索とフィジカルコンピューティング
この分野では、「アンプラグド」(コンピューターを使用しない)な計算層として、多数の参加者を集めて抽象的な点の動きを人間の群れとして再現し、そこから新たな思考を導き出す試みがなされています。これは、ジャドソン・チャーチ・グループの実験的アプローチが現代に蘇ったとも言えるでしょう。
実際、多くのフィジカルコンピューティング研究者がブラック・マウンテン・カレッジの実験を参照しています。ロバート・ラウシェンバーグ、ジョン・ケージ、マース・カニンガムらが参加したこの芸術学校は、後のジャドソン・チャーチの活動に大きな影響を与えました。
クリエイティブ・コーディングやアルゴリズミック・アートの原理を、コンピューターから離れて現実世界で実験的に適用した例として、ナオミ・レオナードとスーザン・マーシャルによるダンス/エンジニアリング・パフォーマンス「Flock Logic」(2010)が挙げられます。この作品は、計算的思考とダンスの融合を体現した先駆的な取り組みとして評価されています。
ここでは公開されている論文を和訳しました。
原文はこちら: In the Dance Studio: An Art and Engineering Exploration of Human Flocking
ダンススタジオで:アートとエンジニアリング
人間の群れの探求?
ナオミ・E・レナード、ジョージ・F・ヤング、ケルシー・ホッホグラフ、ダニエル・T・スウェイン、アーロン・トリッペ、ウィラ・チェン、キャサリン・フィッチ、スーザン・マーシャル、アーロン・トリッペ、ウィラ・チェン、キャサリン・フィッチ、スーザン・マーシャル
プリンストン大学、プリンストン、ニュージャージー州08544、米国
概要
概要 群れロジックは、群れをモデル化するために使用されるフィードバックの法則が、ダンサーに適用されたときにどのように変換されるかを探求するために、アートとエンジニアリングのプロジェクトとして開発された。芸術的な目標は、設計されたフィードバックとインタラクションでマルチエージェントシステムのダイナミクスを活用する振付ツールを作成することでした。工学的な目標は、個々のダンサーが何をするのか、そしてグループレベルで何が生まれるのかを調べることで、人間の群れ、動物の群れ、ロボットのネットワークなどのマルチエージェントシステムに対する洞察と設計原理を提供することでした。ダンスを創作し、集団運動を調査する方法について述べる。ダンサーが隣人との結束と反発の単純なルールに従って動く実験のビデオを分析する。規定のインタラクション・プロトコルと追跡された軌跡を用いて、誰が誰に反応しているかを定義する時変グラフを推定する。グラフ内のノードの状態を計算し、リーダーの出現を示す。結果と今後の方向性について議論する。
キーワード: 集団運動、ダンス、振り付け、フィードバック、社会的相互作用、ネットワーク、リーダーシップ、人間集団、動物集団
1 はじめに
ダンサーのネットワークにおける相互作用と反応のルールが、集団の複雑な創発的集団運動を生み出す。
群れや群れの顕著な集団運動は、決められた振り付けでもなく、指名されたリーダーでもなく、むしろ各個体が従う単純な反応規則から生じるのだ[2]。これらのフィードバック・ルールは、それぞれの個体が、近くにいる個体の相対的な位置や動きに反応してどのように動くかを支配している。例えば、基本的な群れのルールには通常、凝集的な要素と反発的な要素がある[3]。凝集的要素は、各個体が動き回る間、他の数個体から快適な距離を保つことを要求し、反発的要素は、各個体が近づきすぎる他の個体から離れることを要求する。観察される動物集団の複雑な集団運動が、フィードバック規則、集団内の社会的相互作用の力学、集団全体の情報分布、空間的周囲の特徴、個体間の違い、測定値のノイズ、意思決定における不確実性からどのように生まれ、どのように影響を受けるかを説明することに、活発な研究分野が集中している[4, 5]。例えば、ムクドリの群れに関する様々な研究は[6-8]を参照。
群れロジックは、ダンサーのグループが空間を一緒に動き回るときに、これらの法則や関連するフィードバックの法則を適用するとどうなるかを探求した。群れロジックの研究では、群れのルールは規定されているが、ダンサーがどのようにルールを適用するか、またどの程度ルールに忠実に従うかはコントロールされていない。例えば、コヒーレンス・ルールにおける隣人の数と隣人との距離は規定されていたが、ダンサーには、どのようにコヒーレンスする相手を選ぶか、方向が異なる隣人の中でどのように優先順位をつけるか、また、あるダンサーとコヒーレンスすることが他のダンサーに近づきすぎることを意味する場合などの衝突をどのように処理するかは指示されていなかった。また、ダンサーがルールを破ることもあった。このように、人間の群れの創発は、ダンサーの選択とダイナミクスの、規定された特徴と個別化された特徴の両方、つまり未知の特徴によってもたらされた。このように、群れロジック・プロジェクトは、未知のものばかりが存在する野生の動物の群れを研究することと、処方箋に依存した群れをコンピューターでシミュレートすることの中間に位置する、創発的な集団行動を探求する枠組みを提供したのである。
群れロジックのこの側面は、芸術、工学、科学の統合的課題に特に適していた。一方では、群れロジックのフレームワークによって、自然の偏り(この場合は人間の偏り)が集団運動に及ぼす影響や、集団全体の異質性を観察することが可能になった。身体的特徴、性格、ダンスの訓練などが異なるダンサーは、互いに異なる反応を示し、ルールの優先順位や対立の解決方法も異なるだろう。このことは、グループ内の情報の流れや、グループ全体としての外力への対応に影響を与えるだろう。一方、「群れの論理」のフレームワークでは、規定のルールのパラメータが集団の動きに与える影響を体系的に調べることができた。これは、動物の群れを表現するためのルールや環境のパラメータに適用された。例えば、「An Art and Engineering Exploration of Human Flocking(人間の群れの芸術と工学的探究)」3では、まとまるべき相手の数、集団の総人口、集団全体の情報や嗜好の利用可能性、障害物の形、大きさ、配置などが挙げられる。これは、必ずしも動物の群れを表現するためではなく、むしろ芸術的・工学的なデザイン目標に動機づけられたルールや環境のパラメータにも適用された。動物の群れで想定される以上のルールや環境の特徴を変化させることで、個体レベルの行動が、より一般的に、集団レベルの行動の美学や創発的な機能性にどのように結びつくかを探ることができた。そしてこれは、幅広い芸術的、工学的デザインの可能性を生み出すことにつながった。
レナードの工学的目標は、ダンサーとの探求を利用して、動物の群れや人間の群れのダイナミクスのメカニズムや、自然集団やロボット集団の制御のための設計原理についての洞察を得ることだった。この点で、ダンススタジオは実験的な実験台と見なせるだろうか?収集された人間のデータは、さまざまな集団行動の説明に役立てることができるだろうか?ダンサーたちは、衝突を避けようと境界のある空間を移動する人間の群衆を表すことができる。同じように、スタジオの中で隣人や環境に反応しながら動くダンサーは、群れの集団的な動きに合理的な近似性を与える。スタジオの壁は木々や地形のようなもので、ダンサー間の不均一性(経験、身長、自信)は群れのそれと似ている[9]。さらに、ダンサーは身体的に意識するように訓練されており、多くのフィードバックルールを快適に扱うことができるため、この種の探求に特に適している。このように、このセッティングは、扱うことができる質問の種類に非常に大きな柔軟性をもたらした。例えば、本章では、人間の運動データを用いて、ネットワーク内の個体間の影響力がどのように分布し、それが個体の空間分布の変化やグループレベルの形状と運動のダイナミクスにどのように反映されるかを厳密に研究している。これは例えば、人間の群衆が雑然とした空間でどのように動くか、また動物が捕食者に対する脆弱性を減らすためにどのように自分自身を組織化するかについての洞察につながる可能性がある[10]。これはまた、異種ロボットのロバストで応答性の高いネットワークを設計するための、生物学にインスパイアされた手法につながる可能性もある[11]。
人間の集団運動については、動機づけとなる補足的な科学的研究が数多くあり、その多くは群衆力学に焦点を当てている。人間の群衆におけるリーダーシップと意思決定に関する実験は、[12]で述べられている。13]では、自然な歩行者の集団運動の分析により、社会的相互作用が群衆力学に及ぼす影響を明らかにした。14]では、進化力学を利用した人間の集団行動の設計手法が紹介されている。15]では、ヘビーメタルコンサートのビデオデータから観察された、モッシュピットやサークルピットにおける人間の集団行動を予測した。
レナードの工学的目標は、マーシャルの芸術的目標と緊密に統合されていた。マーシャルは2010年にレナードに、群れる動物の集団の動きを支配するルールをダンサー集団が持っていたらどうなるかを調べる調査とコースの可能性について打診した。マーシャルは、集団運動の分散制御に関するレナードの研究をダンサーに応用することで、個人や集団の意識を発達させるための振付ツールやトレーニングツールが生まれる可能性があると考えた。彼女はまた、サイトスペシフィックな大集団パフォーマンス作品を、場所とルールだけで開発することも想像した。
マーシャルの興味は、集団の結束や外的圧力への対応に関連するような群れのルールを、ダンサーのための即興的な指示に変換したいという願望にあった。これらのルールは、個々の相互作用から生まれる予期せぬ複雑な組織化された集団運動をサポートできるのだろうか?有機的な群れの見慣れた外見に似つかわしくない創発的な振り付けを作るために、局所的な感知ルールを振り付け的にどのように変えることができるだろうか?これらのルールをダンサーでなくてもすぐに習得して、フラッシュモブ・パフォーマンスのようなものを作ることはできるだろうか?
演劇とダンスには、構造化された即興とルールとゲームに基づいた動きの実践とパフォーマンスの長い歴史がある[16]。多くの場合、即興的なダンス作品では、個人には幅広い選択肢が開かれており、自分の身体だけでなく舞台全体に対して構成的な責任を負う。しかし、群れのルールは、個人の選択を身近な人に限定し、グループの振付の責任を放棄させる傾向がある。しかし、それにもかかわらず、豊かな集団振付が生まれる。包括的な振付の目標を知らないダンサーが、このツールを使って複雑で組織的なパターンを創り出せるようなルールはできないだろうか?
人間の群れを作り出すために、ダンサーたちは空間を動き回り、あらかじめ定義されたルールに従うよう求められた。団結を可能にするため、各ダンサーには、腕の長さほどの距離に隣人をm人保つというルールが与えられ、m人の隣人の選択は自由に変えることができた。反発を可能にするため、各ダンサーはどのダンサーも腕の長さ以上に近づけないように求められた。つまずきを防ぐため、ダンサーは後方への移動を避けるよう求められた。
これら3つのルール(結束、反発、後方回避)は、最も基本的なルールとして検討された。この3つの基本的なルールのバリエーションも、さまざまな追加ルールや代替ルールと同様に規定された。例えば、隣人との整列、障害物や壁への対応、特定の動きを開始したり模倣したりするオプションなどのルールが実装された。より複雑な情報構造が課された。たとえば、グループ内の2人または3人のダンサーに、特定の場所に移動する、特定のパターンに従って移動するなどの追加ルールが密かに与えられた。ダンサーたちはまた、ダイナミックカバレッジや追跡・回避など、他の種類の行動のルールも実行した。各ダンサーの動きは比較的規定が緩やかだったこともあり、スピード、動きに対する向き、隣人の選択、隣人との位置関係、壁や障害物への対応など、個人差がかなりあった。
複雑で芸術的に満足のいく集団行動が日常的に観察された。2010年のプリンストン大学のアトリエ・コースの一環として、約50人のボランティアが、凝集、反発、整列に関するいくつかのローカルルールと、障害物、壁、「捕食者」に対する反応を簡単に指導された後、それぞれ異なる場所で2回の群れ行動に参加した。レナードとマーシャルから見れば、これらは非常に満足のいくパフォーマンスだった。あるパフォーマンスのスナップショットを図1に示す。イベントのビデオクリップは公開されており、Flock Logicのウェブサイト[1]から、または以下のリンクから直接アクセスすることができる:
http://vimeo.com/19361231(これはリンク切れです)
Video: ‘Flock Logic’ unites science and dance (Evelyn Tu);

この章では、Flock Logicの探求と、芸術的および工学的な調査に使用したツールについて説明する。例として、13人のダンサーがダンススタジオ内を動き回りながら、群れのルールである凝集と反発に従った実験を検証する。頭上のビデオカメラから追跡された軌跡と所定の相互作用ルールを用いて、誰が誰を感知しているかを時間の関数として符号化する時変グラフを推定する。グラフの各ノードの時変ステータスを計算し、あるダンサーが他のダンサーからどれだけ注目されているかを定義する。我々は、その意味、未解決の問題、そして芸術的・科学的な更なる方向性について議論する。
セクション2では、オンラインFlockMakerソフトウェアツールや群れ実験を含む、我々の群れ実験について説明する。3章では軌道追跡について説明します。セクション4では、グラフと、グラフを可視化するツールであるFlockGrapherについて説明します。セクション5ではネットワークの時変グラフを推定する。セクション6ではノードのステータスを推定し、個人の影響力について議論する。セクション7では、結果の考察と、フロック・ロジック・プロジェクトに基づくさらなる芸術的・工学的機会についての考察で締めくくる。
本論文の以前のバージョンは、2012年6月にカナダのモントリオールで開催されたAmerican Control Conferenceのプロシーディングに掲載された[17]。この会議では、100人の会議参加者が人間の群れのパフォーマンス・イベントに参加する特別なインタラクティブ・セッションが開催された。
2人間の群れ
2.1 探索
典型的なフロック・ロジックの探求は、10人から15人のダンサーがダンススタジオを数分間動き回り、レナードとマーシャルが規定した群れのルールを適用するというものであった。このような探索の多くは、1回のセッションの中で連続して行われ、様々な群れのルールが規定された。ダンサーたちは、グループを外から見る機会を頻繁に与えられ、グループの中から見てどう感じるか、グループの外から見てどう見えるかを話し合った。ダンサーたちは日常的に提案し、何度かのセッションの間に、少人数のグループが自分たちのため、そして他のグループのためのルールをデザインした。ダンサーたちが群れのルールに従って動く経験を重ねるにつれ、探求は進化していった。特に学期後半には、ボランティアダンサーが短期間「トレーニング」を受け、群れのグループに加わった。グループにダンサーを加えることで、ダンサーの人数の役割も探求された。セクション2.3で説明するスタジオでの実験では、24人ものダンサーが参加した。2010年12月に行われたフロック・ロジックのパフォーマンスでは、50人以上が参加し、その後のアメリカン・コントロール会議のモントリオールでの特別セッションなどでは、100人以上が参加した。また、セッションは屋外で行われ、境界のない空間での探求の機会となった。基本的な群れのルールである「凝集」(腕の長さ以上の距離を保つこと)、「反発」(腕の長さ以上の距離の人からは離れること)、「後方回避」が、多くの探究の基礎となった。2人の凝集力(m=2)は、平面的な群れや学校のようなものを作るのに十分だった。m = 2の場合、ダンサーは規則正しい間隔を保ち、極性運動、つまり全員が一緒に一方向に動く運動と、円運動、つまり集団が円の周りを動く運動を見せた。円運動は時に漂流し、時に一人の静止したダンサーを中心に固定されたままであった。また、運動量が大きく変化するだけでなく、分裂や融合も起こった。mをm=1、つまり一人でのまとまりに減らすと、結果はより「パレード的」になり、自然の群れのような分散した様子はかなり少なくなった。
壁の存在と障害物の導入を利用した調査が行われた。壁や障害物に特別なルールがないため、ダンサーたちは動物が壁や障害物を扱うのと同じように扱った。あるケースでは、椅子の列が壁から部屋の中央まで一直線に伸びていた。ダンサーたちは、椅子と平行する壁によって作られた狭い空間に移動すると、潮だまりに巻き込まれるように一時的にそこにとどまり、方向が反転してから外に出る。壁や障害物に関してルールが規定されると、生物学的な動機に基づくものではない、さまざまな興味深い集団行動が出現した。例えば、壁には魅力的な引力と「粘着性」が与えられた。その結果、壁に近づいたダンサーは集団から引き離され、そこから動けなくなった(図1参照)。その結果、壁に近づいたダンサーは集団から引き離され、そこから抜け出せなくなった(図1参照)。これは、ダンサー同士がまだ凝集と反発のルールを適用しているため、整然と剥がれたりくっついたりしているように見えた。
別のケースでは、オープンスペースに丸テーブルを移動させ、スリングショットの特性を持たせた。ダンサーはテーブルに近づくと、その周りを一定の方向、例えば反時計回りに、速度を上げて回り、そして “投げ飛ばされる”。ダンサーによってコンフリクトの解決方法が異なるため、これはさまざまな結果につながった。例えば、ラウンドテーブルを使った初期の演技では、最初の数人のダンサーはテーブルの周囲を高速で移動したが、その後は速度を落とし、ゆっくりと動く群れの近くに集まる傾向があった。その後、テーブルの周囲を回るダンサーたちは、この群れの間をすり抜けるのを避けるために立ち止まるか、反発の法則を破って突き進んでいった。2010年12月のパフォーマンスイベントでは、2台のパチンコ台で「滝」効果が持続した(図1参照)。
また、個々の嗜好や目的を規定する能力も探求された。これらの探求は、集団における嗜好や目的の異質性の役割、個人が運動を通じてリーダーシップを発揮できるかどうか、またどのように発揮できるか、そしてその結果生じうる集団的な運動パターンの範囲を理解することへの興味によって動機づけられた。すべてのダンサーは3つの基本的な群れのルールに従うよう指示され、2、3人のダンサーは他のダンサーに知られることなく、特定の追加ルールに従うよう指示された。例えば、選ばれた2~3人のダンサーには、部屋の隅やドアの外に向かうようにといった同じ追加ルールが与えられることもあった。あるいは、2~3人のダンサーに相反するルールが与えられることもあった。たとえば、あるダンサーは部屋の隅を目指し、別のダンサーは反対側の隅を目指すように指示された。あるいは、2人または3人のダンサーに、グループを小グループに分けるなどの共同目標を与えた。私たちは、ダンサーがどのように追加の目的を達成しようとしているのかを探り、自分の動きによって他のダンサーに影響を与えることに成功するダンサーとそうでないダンサーがいることを観察し、議論した。
いくつかの実験では、1人か2人のダンサーに、手やTシャツを振ったり、自転車のライトを点滅させたりして、捕食者や追跡者のように振る舞うよう指示した。この場合、ダンサーは追っ手から安全な距離、例えばスタジオの大きさにもよるが、5フィートか10フィートの距離を保つというルールが与えられた。こうして追っ手は群れにプレッシャーをかけ、群れを閉じ込めたり、群れの形を整えたり、群れの動きをスタジオ内の変化する空間の通路に制限したりすることで、さまざまな美しいパターンを作り出すことができた。また、追撃と回避の循環も検討され、すべてのダンサーに追撃する他のダンサーが1人ずつ割り当てられ、各ダンサーが追撃する人と回避する人を持つ閉じた循環が作られた。モーション・パターンは、[18]で予測されたような定性的な特徴を持つ、複数の交差点を持つ絶えず変化するループであった。図2は、24人のダンサーがダンス・スタジオで行った周期的追跡実験のスナップショットである。

私たちは、任意の整列ルールを加えることで、さらなる芸術的なバリエーションとオプションが生まれることを発見した。また、基本的な群れのルールの代わりに、他の多くのルールも検討した。これらは、芸術的、工学的、科学的な目標に大きく貢献した。例えば、各ダンサーが振動するような速度で動き、加速と減速を繰り返し、その振動が近くにいる他のダンサーと位相がずれるようなルールが適用された。これは、魚の群れで観察される振動速度と、このルールを使って設計できる豊富な運動パターン群によって動機づけられた[19]。別の例では、ダイナミックカバレッジのためのルールが探索された。これらのルールは、分散した資源の空間を探索する問題によって動機づけられた[20]。
2.2 FlockMaker
FlockMakerは、Flock Logicプロジェクトを支援するために開発されたJava WebStartアプリケーションで、集団運動のシミュレーションと探索のために設計されています[21]。FlockMakerは好奇心旺盛な素人でも直感的に操作でき、群れのルールや初期設定の複雑な組み合わせをモデル化することができます。このモデルでは、各ダンサーは、水平面内を可変速度で移動する単一の粒子として表現される。速度と対向角(加速度は含まない)は、時間的にほぼ連続であると仮定される。シミュレーションのユーザーは、”誰かを追いかける”、”隣人を撃退する”、”近くの隣人を減速させる “など、様々な群れのルールをダンサーに割り当てることができます。さらに挙動を制御するために、ユーザーはダンサーのルールや初期設定に関連するさまざまなパラメータ(感知半径、感知した近隣の数、最大回転速度、加法的ランダムノイズの大きさなど)の値を設定することができます。異なるルールを異なるダンサーに割り当てることができる。さらに、各ダンサーは一度に複数のルールに従うように割り当てることができ、各ルールは優先度を表す異なる相対的な重みを持つ可能性がある。
ダンサー同士だけでなく、ダンサーが移動する部屋(4つの壁に囲まれた長方形の空間)とも相互作用します。FlockMakerのユーザーは、部屋の大きさを変えたり、部屋に障害物を追加したり、部屋の特定のゾーンだけに適用されるルールを追加したりすることができます。
プリンストン大学アトリエコースの学生たちは、数週間のアトリエでの作業の後、アトリエで試されたアイデアをテストしたり、新しいアイデアを調査したりするために、FlockMakerを使って時間を過ごしました。FlockMakerで調査されたルールセットや創発的な動作のいくつかは、その後スタジオでも調査されました。
2.3 実験
2010年12月中旬、プリンストン大学の62’7″ x 28’4 “のニューサウス・ダンス・スタジオで、一連の群れ実験を行った。ダンサーのグループは、初期条件、ダンサーの数N(13人または24人)、結束のための隣人の数m(1人または2人)を操作しながら、群れの3つの基本的なルールを実行した。隣人とのアライメントもテストされ、さらに2人のダンサー(他のダンサーは知らない)に、グループを分裂させるという追加ルールが割り当てられた。また、ダンサーが周期的追跡のルールを実行する実験もいくつか行った。
ローカルの有線ネットワークで同期された6台のTrendnet IP-600カメラは、ダンサーの動きを記録するために固定された場所に設置された。台のカメラはスタジオの両端近くの天井に吊るされ、互いに内側を向いている。カメラの視野はスタジオの空間の大部分をカバーし、大きく重なっている。内蔵のソフトウェアを使ってカメラはビデオを録画し、ノートパソコンに保存した。ビデオの解像度は640×480、1秒間に20フレームだった。
2010年12月の一連の実験では、6台のカメラのうちの1台(天井に固定された2台のうちの1台)ですべてのダンサーの動きを完全に捉えられるように、部屋の一部を塞いだ。ダンサーは軌跡の追跡を助けるために、明るい色の帽子をかぶり、黒い服を着て、裸足になった。この章では、2人のプロ・ダンサーと11人の学生からなるN=13人のダンサーの実験を検証する。13人のダンサーは全員、m=2の隣人に対して凝集性をもって群れるという3つの基本的なルールに従うことだけを求められた。実験の総時間は185秒で、音楽の開始から停止までの時間に相当する。我々はこの実験の最初の72秒間のダンサーの追跡された軌跡を研究する。
3 軌道追跡
軌道は、実験の最初の72秒間、1台のカメラからのオーバーヘッド映像にカスタムトラッキングソフトウェアを適用して推定した。追跡された軌跡は、13人のダンサーそれぞれについて、1440個の平面位置ベクトル(x, y)の順序付けられたセットから構成される。速度ベクトルは、時間ステップごとに、位置ベクトルを差分することによって各ダンサーについて計算される。速度と方位は、速度ベクトルの大きさと角度として計算されます。図3は、トラッキングされた位置と動きの方向を重ね合わせたビデオからの1フレームです。
カスタムトラッキングソフトウェアは、我々が開発し、複数の魚やロボットを含む実験に成功したリアルタイムトラッキングアルゴリズムの修正版を使用しています[22]。このアルゴリズムはMADTraC C++ライブラリ[23]を使用して実装されており、低レベルの画像処理ルーチンにはOpenCV[24]を使用しています。オリジナルのトラッキングソフトウエアは、密に分布している可能性のある、外観が互いに非常に似ているオブジェクトをトラッキングするという課題に対処するために設計されました。そのため、ダンサーの軌跡を推定するタスクに適用可能でした。
トラッキングアルゴリズムは3つのステップに分かれており、各ビデオフレームに対して繰り返し行われます。最初のステップでは、画像セグメンテーションにより、各ブロブがダンサーの帽子に属する可能性の高い連続したピクセルの集合であるような「ブロブ」の集合を生成します。尤度はHSV色空間で各画素の値を閾値処理し、2値画像にマッピングすることで決定される。ブロブは、[25]に基づくOpenCVの内蔵ブロブラベリングアルゴリズムを用いて2値画像から抽出されます。ブロブは、ダンサー同士の物理的な近さ、カメラの角度による画像内のダンサーの近さ、画像内のノイズなどにより、複数のダンサーに関連付けられることが多い。
第2ステップでは、各ダンサーの位置に関するノイズの多い測定値を抽出するためにブロブを分析する。1人のダンサーが1つのblobに関連する場合、そのダンサーの位置の測定値は、そのblob内のすべてのピクセルの重心とみなされます。そうでない場合は、複数のダンサーのブロブや、間隔が密集したブロブのクラスターを解決するために、期待値最大化混合ガウシアン(mixture-of-gaussian)を使用する。

(EMMG)アルゴリズムが使用され、与えられたクラスターに対してダンサーの位置を反復的に調整し、位置測定値を出力として提供する。
第3のステップでは、ノイズの多い位置測定値を、各ダンサーについて、現在のフレームのより正確な推定位置(x,y)を提供し、次のフレームの位置を予測するために、uncented Kalman Filter(UKF)とともに使用する。各ダンサーの推定位置は、ダンサーの追跡軌跡の現在点として保存されます。予測された位置は、次のトラッキングの反復を通知するために使用されます。(x,y)位置ベクトルは床に平行な座標フレームで表現されます。画像平面座標からこれらの座標への変換は、シーン内の既知の位置に配置された複数のオブジェクトの画像にカメラキャリブレーション技術を適用することで決定された。各ダンサーの平均身長は1.65メートルと仮定。
4 グラフ理論と可視化
4.1 グラフの背景
ダンサーの数をNとする。各ダンサーiについて、ダンサーiによって位置が観察され、結束に使用されるダンサーの集合を隣人集合Ni と定義する。
ここで、V = {1, 2, … , N}はノードの集合である。N}はノードの集合、E⊆V×Vはエッジの集合、AはN×Nの隣接行列であり、エッジ(i,j)∈Eのときai,j=1、それ以外のときai,j=0である。グラフの各ノードはダンサーに対応し,グラフはj∈Niのとき辺(i, j)を含む.辺(i, j) ∈ Eは,(j, i)もEに含まれる場合は無向グラフ,そうでない場合は有向グラフである.グラフが無向グラフであるのは、すべての辺が無向である場合、つまりAが対称である場合であり、そうでない場合は有向である。
グラフは、各節点に点を、各辺に適切な対の節点間に線を引くことで視覚的に表現できる。無向辺は一般に単純な線で描かれ、有向辺(i, j)はノードiからノードjを指す矢印で描かれる。
Gのパスは、繰り返しを含まず、各ノードが前のノードの近傍にあるようなノードの(有限)シーケンスである。パスの長さは、パスが通過する辺の数で与えられる。グラフのノードiとjの間の距離di,jは、iからjへの任意のパスの最短距離である。di,jは必ずしもdj,iと等しくないので、この距離は計量ではない。
グラフGは、大域的に到達可能なノードkを含んでいれば連結されている;すなわち、すべてのノードiに対してiからkへのパスがG中に存在する。Gの強連結成分とは、ノードの最大部分集合であり、その部分集合のすべてのノードの対の間にGのパスが存在するようなものである。すべての有向辺を無向辺で置き換えたときに連結される場合、G は弱連結である。弱連結成分とは、Gのすべての有向辺を無向辺で置き換えたときに連結成分を形成するノードの最大部分集合である。
すなわち、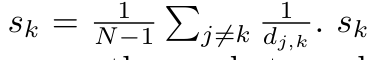 は、他のすべてのノードからノードkへのエッジがある場合は最大(1に等しい)となり、ノードkにつながるエッジがない場合は最小(0に等しい)となる。
は、他のすべてのノードからノードkへのエッジがある場合は最大(1に等しい)となり、ノードkにつながるエッジがない場合は最小(0に等しい)となる。
和訳する際に記号がおかしいので原文の画像も貼っておきます。

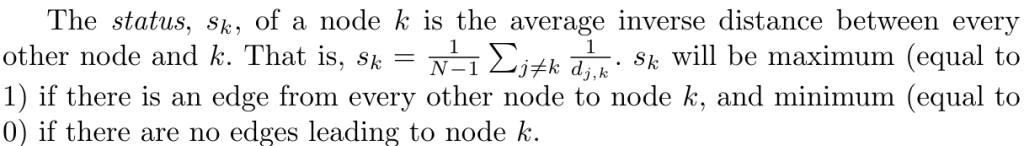
4.2 グラフの可視化
FlockGrapherは、群れの位置データから得られる様々な種類のグラフを計算、視覚化、評価するMatlabツールである。グラフィカル・ユーザー・インターフェースを用いて、群れの個体の追跡された位置と運動方向のデータを2次元または3次元で受け付ける。ある特定の瞬間のデータを可視化することも、連続する時間ステップに対応するデータセットの時系列アニメーションを作成することもできる。ユーザーは、個体の近傍を所定の最近接数または所定の感知半径で定義することにより、データからグラフを作成することができる。ノードの移動方向を含むデータの場合、FlockGrapherは、個体の移動方向について対称であると仮定した、制限された視野角を組み込むことができます。固定の最近接数と制限された視野角の場合、ノードから見える近傍の数が必要な数より少ない場合、十分な近傍が見えるまで視野角は移動方向に対して回転します。エッジの重みは、例えばノード間の距離の関数として自動的に操作することもできるし、ユーザーによって規定することもできる。
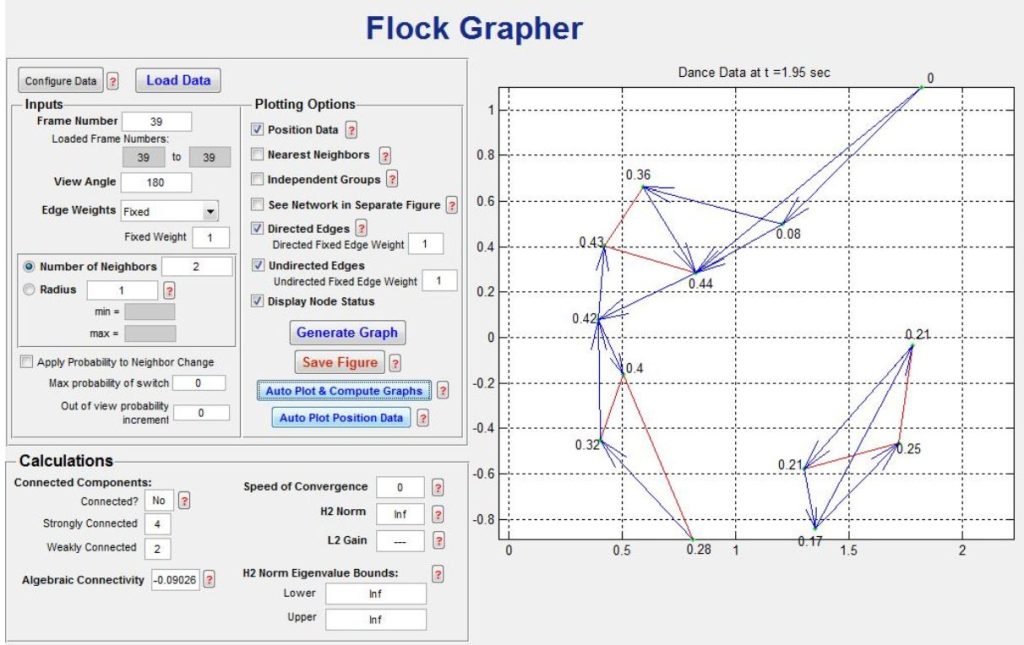
センシンググラフが計算されると、FlockGrapherは、強結合と弱結合の構成要素の数、代数的結合性、収束速度、ノードの状態など、さまざまなグラフ特性を評価することができます。例えば、有向エッジと無向エッジを異なる色で区別することができます。連続する時間ステップに対応するデータ集合については、グラフの可視化が変化するにつれて、これらのプロパティの時間変化値が表示される。人間の群れ実験の場合、この動的グラフ可視化をダンサーのビデオと同時に実行し、計算された行動と観察された行動を比較することができます。FlockGrapherは計算されたすべてのデータを保存することができ、さらなる分析を可能にします。FlockGrapherのスクリーンショットを図4に示す。グラフとそのプロパティは、図3に示したビデオのフレームに対応している。
5 センシング・モデルとグラフ計算
各ダンサーには同じ特定のルールが与えられているため、追跡データに同じルールを適用し、ダンサーが使用したセンシンググラフを再構築することは原理的には可能である。しかし、ルールと人間の行動のある側面が、このタスクを困難にしている。ダンサーはそれぞれ、他の2人のダンサーから腕の長さ分離れるように指示されているが、この2人の隣人をどのように選ぶかについては指示されていない。さらに、人間の視野は200◦まであるが[27]、ダンサーは常に両隣のダンサーが見えるようにしておかなければならないという強制力はなかった。
このような制約があるため、ダンサーのセンシング・グラフを推定するために、2つの重要な仮定を置く。第一に、各ダンサーは進行方向を中心とした限られた角度範囲内からしか隣人を選ばないと仮定する。頭を急速に動かしているダンサーは観察されなかったので、動きの方向は頭の方向、したがって視野範囲の中心の妥当な代理であると仮定する。この仮定は一般的にデータに当てはまりますが、ダンサーが自分の向いている方向と違う方向に動いたり、頭を体に対して一定の角度に向けたまま動いたりする例が観察されました。このような現象は、私たちのポイント・トラッキング・アプローチでは検出不可能ですが、各ダンサーの顔の向きを検出する機能を持つ、より洗練されたトラッカーであれば説明できるかもしれません。第二に、各ダンサーは、この範囲内で最も近くにいる2人とコヒーシヨン・ルールを適用していたと仮定することから始めます。すべてのダンサーは、2人の隣人を腕の長さに保とうとしているので(腕の長さより近いダンサーはいないようにする)、ダンサーの隣人は当然、他のダンサーの中で最も近くにいるダンサーになる。
このような前提のもと、私たちはFlockGrapherを使って、限られた視野角で2近傍グラフを計算することで、各時間(フレーム)のセンシンググラフを推定しました。他のダンサーが2人以下しか見えない場合、動きの方向を使って視域の中心を決め、2人のダンサーが見えるようになるまで視域を回転させた。しかし、どのような視野角を選べばダンサーの行動を最もよく表現できるかは、事前にわからなかった。
集団行動では、コミュニケーション・グラフがつながっていない場合、集団が一緒にいることを保証することは不可能である[28]。グラフが切断されている場合、異なるサブグループが異なる方向に移動し、グループが分裂するのを防ぐものは何もない。しかし、環境の他の特徴(部屋のスペースが限られているなど)により、グループを元に戻すことができる。集団の分裂と融合が観察されたので、私たちは、ダンサーの集団が分裂するのが観察されたときにはグラフが切断され、ダンサーの集団が凝集するのが観察されたときにはグラフが連結されたままになるような視角を、センシング・モデルの視角として選択した。
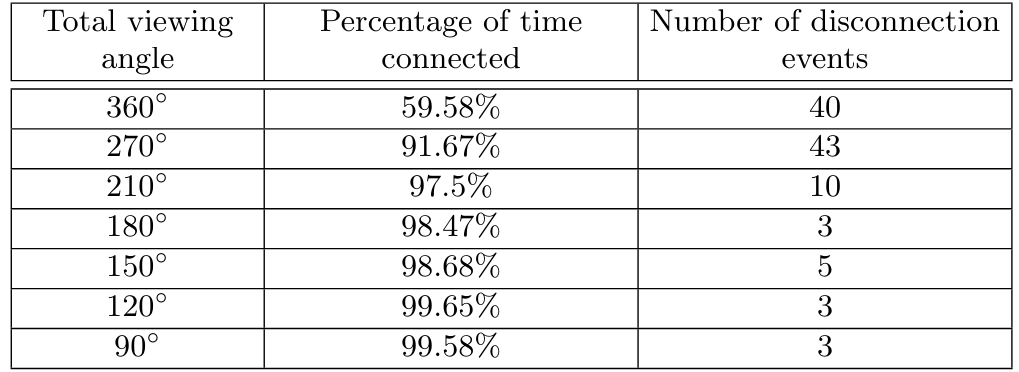
表1は、異なる視野角を使用して、追跡期間全体にわたってセンシング・グラフを推定した結果を示している。視角を360◦から270◦に下げると、グラフが連結している時間が大幅に改善され、視角120◦で連結度が最大になることがわかる。しかし、私たちの目標は、単純に連結度を最大にすることではなく、観察されたグループの行動と一致させることであった。
実験の初期、約1秒から3秒の間に、4人のダンサーからなる小さなグループが他のグループから分裂した。このグループ内のダンサーは、お互いにしか観察していないように見えた。残りの8人のダンサーもグループを形成し、互いのみを観察していた。最後のダンサーは、本来なら両方のグループを観察してから大きなグループに向かうのだが、他のダンサーがこの個人を観察していなかったため、この間ずっとグループは分裂していた。やがて、大きいグループのダンサーが小さいグループを観察するようになり、再びひとつの「群れ」になった。この切断現象は、視野角150◦以上の推定グラフには反映されたが、それ以下の角度では反映されなかった。しかし、視角150◦の場合、映像を直接観察するとまだ群れが分裂しているように見えるが、この間隔内の数点でグラフがつながった。180◦の視野角ではこのようなことはなかった。したがって、180◦がダンサーの分裂行動と最もよく一致するものとして選ばれた。図3は、この切断時のグループの様子を示しており、図4のグラフ(図3のフレームに対応)は、180◦の視野角で計算したものである。
センシング・グラフの最初の推定は、グループ内の分裂をとらえ、追跡された期間の残りの間、接続されたままであるが、真のセンシング・グラフの粗い近似であることに変わりはない。例えば、いくつかのノードは我々の推定グラフの中で急速に隣人を変えているが、これはダンサーが隣人を変える速度の過大評価である可能性が高い。その代わり、ある個体が隣人として選ばれたばかりの場合、その個体は、他の個体が視界に近づいたときにすぐに捨てられるのではなく、一定期間隣人として留まる可能性が高い。急激な隣人変動を減らすために、2つのステップがとられた。まず、追跡された位置データはローパスフィルターに通され、その結果、ノードのヘディングが平滑化された。次に、隣人が選ばれてからすぐに隣人を変えたがらないという個体の性質を考慮し、推定モデルに現在の隣人からより近いダンサーに切り替わる確率を表す項を追加した。この確率が低ければ低いほど、ダンサーがより近いダンサーに切り替える「慣性」が大きくなる。この確率は、新しい隣人が選ばれるたびに低い値にリセットされ、時間が経つにつれて高くなるようにすることで、センシング・グラフのエッジの慣性を捉えることができた。
6 個人の影響力の分析
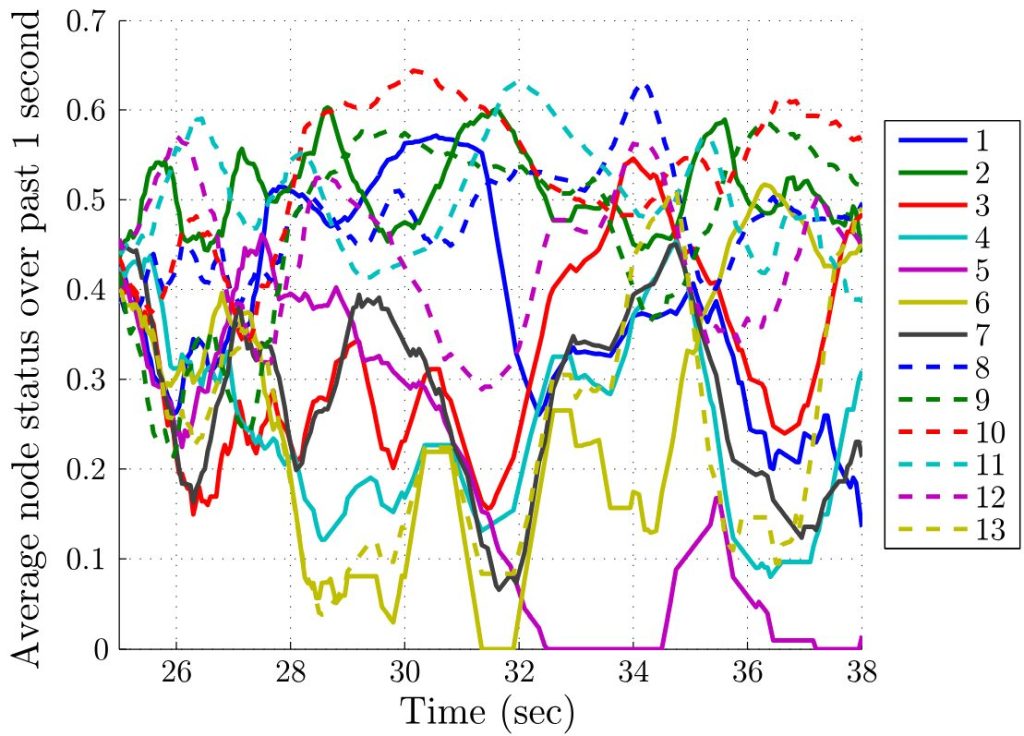
推定された時変センシング・グラフを用いて、グループ内の各個人の影響力の調査を開始する。我々の方法はノードのステータスを計算し、比較することである。各個人がどのように群れルールを実行したかを正確に知ることなく、ノード・ステータスはグループ内での個人の重要性の推定を提供することができる。ステータスが0のダンサーは、グループ内で誰もそのダンサーを観察していないため、影響力を持たない。ステータスが1のダンサーは、他のすべての個人がそのダンサーを直接観察しているため、最大限の影響力を持ちます。しかし、グラフの時間変化の性質により、個人の重要度は現在のノード・ステータスだけでなく、過去のノード・ステータスにも依存します。したがって、瞬間的な重要性の最初の推定値として、各ノードの過去1秒間の平均ステータスを見ることができます。追跡期間の一部の平均ノード・ステータスのプロットを図5に示します。
ノード・ステータスは個人がグループに影響を与える可能性の尺度を提供しますが、その影響力が実際に行使されたかどうかを示すものではありません。したがって、このデータセットにおいて、ノード・ステータスがダンサーの影響力に本当に関係しているかどうかを調べるために、グループの残りの部分に対する個人の影響力の定量的尺度を調査する。この量はリードタイムと呼ばれ、個人の運動方向と集団の運動方向の相互相関関数にピークが生じる時間である。このリードタイムが正の値であれば、ある個体が集団をリードする傾向がある(すなわち、方向を変えてから集団がそれに従う)ことを示し、負の値であれば、ある個体が集団に遅れる傾向がある(すなわち、集団が方向を変えてから集団に従う)ことを示す。我々は、このリードタイムの尺度が平均ノード・ステータスと強く相関し、平均ステータスが最も高いノードが最大のリードタイムを持ち、平均ステータスが最も低いノードが最大のラグタイムを持つことを発見した。したがって、我々のノード・ステータスの計算が、グループ内のリーダーシップの役割についての洞察を実際に提供することを主張する。重要なことは、任意の時点でノードステータスを計算することができるため、群れイベントを通して瞬時に変化するリーダーシップを調査することができるということです。
平均化されたノード・ステータスのプロットを調べることで、ある特定のノードが長期間にわたってグループ内で最大の重要性を獲得した(ステータス値が高い)「リーダーシップ・イベント」を特定することができます。図5では、ノード10が約28.75秒から31.45秒の間にリーダーになったときに、そのようなイベントの1つを観察することができます。ビデオを見ると、この間、グループは部屋の左奥から右手前に向かって移動しており、ノード10がグループの先頭にいたことがわかります。このことは、私たちのノード・ステータス測定が創発的なリーダーシップを捉えることができることを示唆しています。
もう1つのリーダーシップ・イベントは、1人のダンサーが動きを止め、残りのダンサーがこの個人の周りを回り始めた期間にデータから観察することができる。しかし、このイベントで最もステータスが高かったのは、静止していたダンサーではなく、静止していたダンサーのすぐ近くにいて、輪になって動き続けていたダンサーだった。というのも、他の時(ただし追跡期間中ではなかった)には、ひとりのダンサーが止まると、やがてグループ全体も止まってしまうからである。この2種類の出来事の違い(サークリングと静止した集団の動き)は、静止しているダンサーと近くにいるダンサーの状態の違いによるのかもしれない。

追跡された期間全体にわたって各個人のステータスを平均することで、一部の個人がグループに不釣り合いな影響を与えたかどうかをさらに評価することができる。図6は、追跡期間中の各ノードのステータスの平均を示しています。ノード12と10の平均ステータスが最も高く、グループ平均よりも1.9σと1.7σ高いことがわかります。
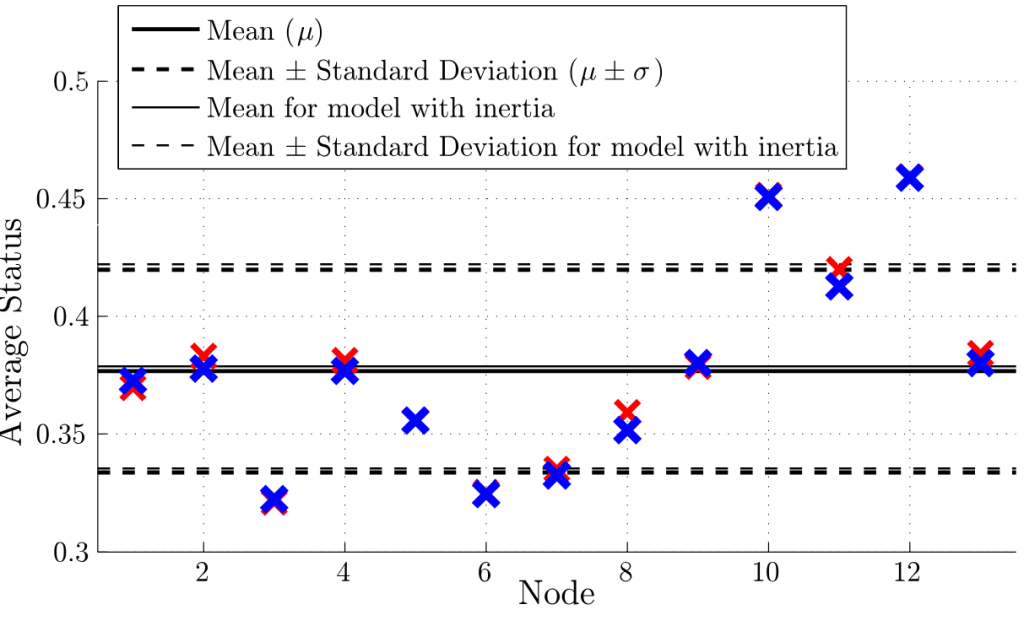
追跡された全期間における個体のステータスの平均は、スイッチングの慣性、あるいは同等に、隣人へのコミットメントをモデル化するために、上で説明したように、隣人のスイッチングに対する確率ベースの消極性を含む場合にも同様に計算することができる。興味深いことに、この慣性の項は1秒あたりの平均的な隣人変更を大幅に減少させますが、平均的なノードステータス値の全体的な構造は大きく変化しません。図6は、元のモデル(青)と慣性項をフィルターにかけたモデル(赤)の両方で、各ノードの平均ステータスを表示しています。2つのモデルの平均ノード・ステータス値の間には多少のばらつきがありますが、同じノードが上下の外れ値を表しています。このことは、隣人交代への消極性をモデルに組み込んでも、ノードの隣人の非現実的な変動を平滑化する可能性はあっても、全体的なセンシング構造、特にリーダーの出現は変わらないことを示唆している。
我々は、図6の異常値ノード、特に非常に高いステータスを持つノードの出現は、人間のバイアスによるものであるという仮説を立てた。これを検証するために、私たちは人間のバイアスを排除したエージェントベースの群れシミュレーションを開発しました。我々の仮説を考えると、人間のバイアスのないシミュレーション・エージェントは異常値ノードを示さないと予想される。シミュレーションは、ダンススタジオのような境界のある空間で、平面上を移動する粒子をモデル化し、ダンサーに与えられたものに近いルールとパラメータ値に従います。シミュレーションは Matlab で実行され、粒子の位置は同期して更新され、180◦ の視野角内にある最も近い 2 つのノードから 1 腕の長さ(0.80 m と仮定)を維持する方向に移動し、同時に 1 腕の長さ内にある他のすべてのノードから反発します。さらに,速度,旋回速度,境界線に対する応答に関する制限を提供するために,追加関数が組み込まれた.これらの各パーティクルの対応するノードのステータスは、ダンサーのステータスと同様に計算された。
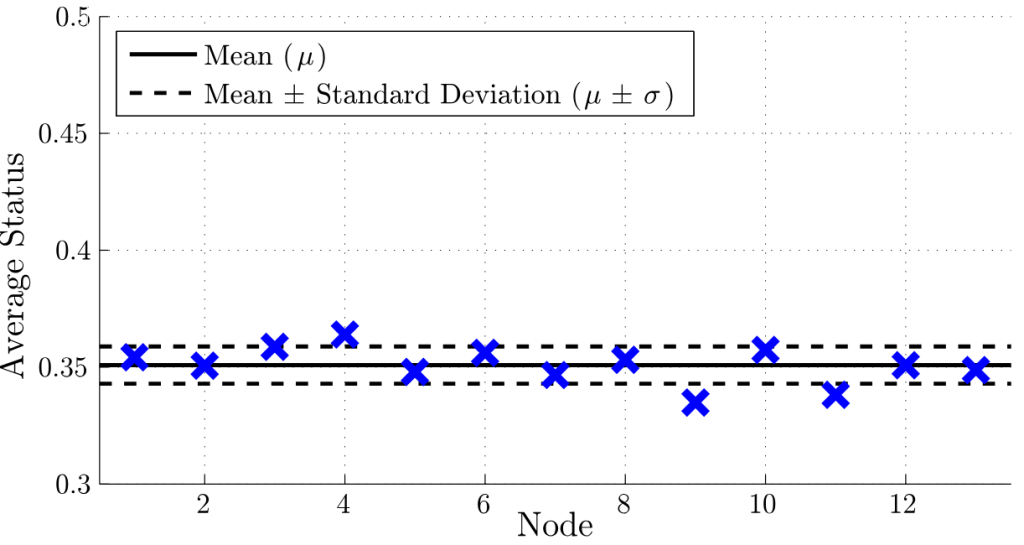
私たちのシミュレートしたシステムは、実験のダンサーと同じ位置とヘディングで初期化され、その後72秒間にわたって各ノードの平均ステータスが計算された。最初の72秒間におけるノードの平均状態は図7に示されており、図6のプロットと比較することができます。図7を見ると、平均と標準偏差の両方が人間のダンサーの場合よりも小さく、さらに有意な外れ値がないことがわかります。シミュレーションのすべてのノードのステータスは、ノードのステータスが最も高かった8位の人間のダンサーより下、10位の人間のダンサーより上の値の範囲にあります。また、ランダムな初期条件で追加のシミュレーションも実行した。ランダムな初期条件でそれぞれ72秒間実行した40回のシミュレーションの平均ステータスは約0.352、平均標準偏差は約0.0094であった。これらの平均値と標準偏差の値は、ダンサーの初期条件を用いた図7のシミュレーションの値(それぞれ0.351と0.0080)と非常によく似ており、追跡されたダンサーのデータから計算された値(それぞれ0.377と0.043)よりもかなり小さい。
この比較は、ダンサーの行動における人間のバイアスの1つの結果として、同一の粒子からなるグループと比較して、ある個人の影響力が低く、他の個人の影響力が著しく高いことを示唆している。このことは、リーダーシップが単にグループ内のランダムな混合の結果として生じるのではなく、一部の個人の行動によって、影響力の高いポジションに就く可能性が高くなることを示唆している。ノード10、11、12(平均ステータスが最も高い3つのノード)に対応するダンサーは、図3と4の小さな切断されたグループにいる4人のダンサーのうちの3人であることに注目したい。
7 最後に
ダンスと制御理論の交差点で構想されたFlock Logicプロジェクトは、集団的な動きを芸術的、工学的、科学的に研究するための斬新で生成的なフレームワークを生み出した。このプロジェクトは、鳥の群れや魚の群れをモデルにしたフィードバック・ルールをダンサーが適用したときに現れる運動パターンの探求と実験を中心に行われた。このフレームワークは、個々の行動と反応に関する規定されたルールと、生命体の未知の選択と行動を組み合わせたもので、部分的にはシステマティックに、部分的にはアンコントロールな探求の機会をもたらした。その結果、群れロジックのフレームワークは、ダンスの芸術的探求や振り付けのためのツールの探求、マルチエージェント・システム・ダイナミクスのための分散制御法則の工学的探求、さらには動物の集団行動や群衆ダイナミクスの科学的探求に役立つことがわかった。
ダンサーは、決められた数の他のダンサーから腕の長さほどの距離を保ち、腕の長さより近くには誰も近寄らせないようにしながら動き回るように指示された。壁、障害物、ゾーンのルールが追加された。追加的な目的と嗜好は選択的に、かつ密かに課され、少数のダンサーは明示的な合図なしに、自分の動きによってのみ集団に影響を与えるよう求められた。追っ手や捕食者として行動するダンサーは、集団にダイナミックな圧力をかけ、しばしば美しい効果をもたらした。アラインメント・ルールを用いて、方向性の同期と反同期が探求された。多くの芸術的な探求は、もともとは動物の行動の観察や分析から、あるいは採食や被覆といった工学的な設計目的から動機づけられた、さまざまな種類のルールを利用していた。また、特定の障害物への対応をデザインするなど、純粋に芸術的な目標に突き動かされた探索もあった。
ダンサー集団の異質性の役割、特に集団運動に対する異なるダンサーの相対的な影響に関する疑問を解決するために、我々は13人のダンサーが2人組の凝集による群れの基本ルールを適用した実験のビデオデータを分析した。ビデオから72秒間のダンサーの軌跡を追跡した。次に、群れのルールをデータに適用し、映像の各フレームにおけるネットワークグラフを推定した。得られた時変グラフから、各フレームにおける各ダンサーのノード・ステータスを計算した。ノード・ステータスは、あるダンサーが他のダンサーからどれだけ注目されているかの指標となる。つまり、ステータスの高いダンサーは通常、他のグループよりも先にターンする。このことから、ノードのステータスが高いということは、影響力が高いということであり、リーダーシップがあるということである。各ダンサーの平均ステータスを追跡区間全体にわたって調べたところ、ステータスが平均値より標準偏差の2倍近く高いダンサーが2人いることがわかった。この結果は、新しく獲得した隣人に対するダンサーのコミットメントをモデル化する慣性項を追加することでロバストであることを示した。また、人間のバイアスが、ダンサー間の影響力の大きなばらつき、特に外れ値を説明する証拠を、人間のバイアスがないダンサーを粒子としてモデル化したシミュレーションの類似結果とデータを比較することで示した。
これらの結果は、さらに多くの興味深い疑問と今後の調査の可能性を提起している。例えば、人間のバイアスはどのようにしてリーダーシップを生み出すのだろうか?特定のダンサーは、他のダンサーの注目を集めるような動きをするのだろうか?あるいは、リーダーとして登場した個人は、例えば指示されたよりも他者に注意を払わないなど、ルールを破っているのだろうか?この結果は、ルールに従うこととルールを破ることの間に興味深い緊張関係がある可能性を示唆している。これは、進化ゲーム理論を用いて科学的に解明できるかもしれない。ルールを破ることは、自分の好みの方向に集団を影響させるという利点があるが、ルールを破ることは、集団生活の利点を失うという代償もある。
その他の疑問は、ルールと環境の関係、そして結果として生じる集団の形と勢いに関するものである。極性運動と円運動を説明するものは何か?集団の分裂や融合を説明するものは何か?さらに多くの芸術的、工学的、科学的な研究が可能であり、基本的な群れのルールをより抽象的で非空間的な領域に拡張することもできる。レクリエーションやセラピーのための人間の群れ作りも研究されるかもしれない。群れロジックのパフォーマンスの参加者は、ゴールのない集団に参加することで心が落ち着き、新しいものを生み出す一員となることにやりがいを感じると述べている。
8 謝辞
アレックス・ホルネスのリードタイム/ラグタイムとノードの状態との相関に関する研究に感謝する。
参考文献
1. Leonard, N. E., Marshall, S.: 群れ論理. (2010) [オンライン]. 利用可能: http://www.princeton.edu/∼flocklogic
2. (2010年) [オンライン]Available∼flocklogic 2. Parrish, J. K., Edelstein-Keshet, L.: 動物集合における複雑性、パターン、進化のトレードオフ. Science. 284:5411, 99-101 (1999)
3. Breder, J. C. M.: 魚群やその他の動物の集合を記述する方程式. Ecology. 35:3, 361-370 (1954)
4. Couzin, I. D., Krause, J.: Self-organization and Collective Behavior in Vertebrates. Advances in the Study of Behavior. 32, 1-75 (2003)
5. Sumpter, D. J. T.: Collective Animal Behavior. プリンストン大学出版局、プリンストン (2010)
6. Ballerini, M., Cabibbo, N., Candelier, R., Cavagna, A., Cisbani, E., Giardina, I., Lecomte, V., Orlandi, A., Parisi, G., Procaccini, A. et al: Interaction Ruling Animal Collective Behavior Depends on Topological Rather than Metric Distance: フィールド調査からの証拠。米国科学アカデミー紀要。105:4, 1232-1237 (2008)
7. このような研究は、「生物多様性」、「生物多様性条約」、「生物多様性条約」、「生物多様性条約」、「生物多様性条約」、「生物多様性条約」、「生物多様性条約」、「生物多様性条約」、「生物多様性条約」、「生物多様性条約」、「生物多様性条約」、「生物多様性条約」、「生物多様性条約」、「生物多様性条約」、「生物多様性条約」、「生物多様性条約」に基づいている。PLoS Computational Biology. 9:1, 1-7 (2013)
8. Hildenbrandt, H., Carere, C., Hemelrijk, C. K.: 自己組織化された数千羽のムクドリの空中ディスプレイ: モデル。行動生態学。21:6, 1349-1359 (2010)
9. ゲロン、S.、レヴィン、S.A.、ルーベンスタイン、D.I.:群れの力学: 個体から集団へ。J. Theor. 182, 85-98 (1996)
10. Behavioral Ecology. 18:4, . 725-729 (2007)
11. また、「動物集団の分岐と行動」(共著)は、「動物集団の分岐と行動」(共著)である。In: このような場合,どのように対処すればよいのだろうか.Elsevier (2013)
12. Phil. (注1)本データはこの商品が発売された時点の情報です。R. Soc. B. 364, 781-789 (2009)
13. このような集団行動は、集団行動と集団行動との関連性を明らかにし、集団行動と集団行動との関連性を明らかにすることを目的としている。PLoS ONE. 5:4, 1-7 (2010)
14. Funes, P., Orme, B., Bonabeau, E.: Shaping Collective Behavior: An Exploratory Design Approach. In: 人工生命 IX: において。第9回国際シミュレーション・アンド・シ Conf. on the Simulation and Synthesis of Artificial Life, pp.232 – 237. MIT Press (2004)
15. ヘビーメタルコンサートのモッシュピットやサークルピットにおける人間の集団運動. Physical Review Letters. 100:228701, 1-5 (2013)
16. Clemente, K.: Playing with Performance: Clemente, K.: Playing with Performance: The Element of the Game in Experimental Dance and Theater. The Journal of Popular Culture. xxiv, 1-10 (1990)
17. Leonard, N. E., Young, G., Hochgraf, K., Swain, D., Trippe, A., Chen, W., Marshall, S.: In the Dance Studio: 人間の群れの分析。In: において。アメリカ制御学会, pp.4333-4338. IEEE (2012)
18. Pais, D., Leonard, N. E.: Pursuit and Evasion: 進化的ダイナミクスと集団運動。In: Proc. AIAA Guidance, Navigation, and Control Conference, pp. AIAA (2010)
19. このような場合、そのような飛行を行うことができるのは、そのような飛行を行 うことができる飛行士だけである。In: このような場合、そのような制御をどのように行えばよいのであろうか。このような場合、”宙返り “と呼ばれる。IEEE (2009) 24 人間の群れの芸術と工学的探求
20. このような場合、「移動センサネットワークのための動的マッピング誤差の対称的カバレッジ」 が必要となる。において: このような場合、そのようなセンサネットワー クは、どのような方法で利用されるのだろうか。このような場合、そのようなネットワークは、どのように機能するのだろうか。IEEE (2011)
21. Chen, W., Leonard, N. E., Marshall, S.: FlockMaker: 集団運動のシミュレータ。(2010) [Online]. 利用可能: http://dcsl.princeton.edu/dance
22. 魚群行動実験のためのリアルタイム・フィードバック制御ロボット魚. を用いた行動実験のための実時間フィードバック制御ロボット魚。100:1, 150-163 (2012)
23. MADTraC Framework Source Documentation. (2011) [オンライン]。利用可能: http://poincare.princeton.edu/MADTraC/docs/
24. Bradski, G.: OpenCV (Open Computer Vision) Library. (2011) [オンライン]。利用可能: http://opencv.willowgarage.com/wiki/Welcome
25. Chang, F., Chen, C.-J., Lu, C.-J: A Linear-Time Component-Labeling Algorithm Using Contour Tracing Technique. Computer Vision and Image Understanding. 93:2, 206-220 (2004).
26. グラフのラプラシアンスペクトル. Graph Theory, Combinatorics and Applications. 2, 871-898 (1991).
27. Werner, E., Rossi: Manual of Visual Fields. チャーチル・リヴィングストン、ニューヨーク (1991)
28. このような場合,そのような問題を解決するために必要なのは,そのような問題 を解決するために必要な情報を提供することである.In: (1)制御と制御。米国制御学会、1859-1864 ページ。IEEE, (2005)